Найти массу однородной пластины ограниченной линиями. Как вычислить центр тяжести плоской ограниченной фигурыс помощью двойного интеграла? Приложения тройных интегралов

Чтобы вычислить величины m, и нужно использовать формулы (4), (5) и (7). В результате получаем формулы для координат центра масс тонкой пластинки :

Пример 4 (вычисление координат центра масс однородной пластинки)

Найти координаты центра масс однородной фигуры, ограниченной линиями и .

Построив фигуру, замечаем, что геометрически она является симметричной относительно прямой Так как фигура изготовлена из однородного материала, то она имеет не только геометрическую, но и физическую симметрию, то есть масса её части, которая расположена слева от оси симметрии, равна массе части, которая расположена справа. Тогда по известным физическим свойствам центра масс заключаем, что он находится на оси симметрии, то есть

Чтобы вычислить , составляем статический момент и используем формулы (4) и (5):

;

Ответ: C .

Приложения тройных интегралов

Приложения тройных интегралов аналогичны приложениям двойных интегралов, но только для трехмерных тел.

Если использовать одно из свойств тройного интеграла (о его значении от функции, тождественно равной единице), то получается формула для вычисления объема любого пространственного тела :

Записываем формулу для объема через тройной интеграл и вычисляем тройной интеграл в цилиндрических координатах:

Ответ: (единиц объема).

Формула для вычисления массы трехмерного объекта, занимающего объем V , имеет вид:

(13)

Здесь - это объемная плотность распределения массы.

Пример 6 (вычисление массы трехмерного тела)

Найти массу шара радиуса R , если плотность пропорциональна кубу расстояния от центра и на единице расстояния равна k .

V : элементарный объем и .

Заметим, что здесь при вычислении трехкратного интеграла получилось произведение интегралов, так как внутренние интегралы оказались не зависящими от переменных внешних интегралов.

Ответ: (единиц массы).

Механические характеристики для объема V (статические моменты, моменты инерции, координаты центра масс) вычисляются по формулам, которые

составляются по аналогии с формулами для двумерных тел.

Элементарные статические моменты и моменты инерции относительно координатных осей:

элементарные моменты инерции относительно координатных плоскостей и точки начала координат:

Далее, чтобы вычислить механическую характеристику всего объёма V ,нужно просуммировать элементарные слагаемые этой характеристики по всем частям разбиения (так как вычисляемая характеристика обладает свойством аддитивности), а затем перейти к пределу в получившейся сумме при условии, что неограниченно уменьшаются (стягиваются в точки) все элементарные части разбиения. Эти действия описываются как интегрирование элементарного слагаемого вычисляемой механической характеристики по объёму V .

В результате получаются следующие формулы для вычисления статических моментов М и моментов инерции I трехмерных тел :

На практике полезно эти формулы не только использовать как готовые, но и выводить их в решаемой задаче.

Примеры 7 (вычисление механических характеристик трехмерных тел)

Найти момент инерции однородного цилиндра, высота которого h и радиус основания R , относительно оси, совпадающей с диаметром основания.

Найдём расстояние d для произвольной точки цилиндра:

расстояние от точки с координатами до оси – это есть длина перпендикуляра, проведенного от этой точки к оси . Построим плоскость перпендикулярную оси так, что точка принадлежит этой плоскости. Тогда любая прямая, пересекающая ось и принадлежащая этой плоскости, будет перпендикулярна . В частности, прямая, соединяющая точку и точку , будет перпендикулярна оси , а расстояние между этими точками и будет искомым расстоянием d . Вычисляем его по известной формуле расстояния между двумя точками.

Приведем пример определения центра массы тела методом разделения его на отдельные тела, центры масс которых известны.

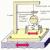
Пример 1 . Определить координаты центра массы однородной пластины (рис.9). Размеры заданы в миллиметрах на рисунке 9.

Решение: Показываем оси координат и . Разбиваем пластину на части, которые образованы тремя прямоугольниками. Для каждого прямоугольника проводим диагонали, точки пересечения которых и определяют положения центров массы каждого прямоугольника. В принятой системе координат несложно найти значения координат этих точек. А именно:

(-1; 1), (1;5),(5;9). Площади каждого тела соответственно равны:

; ; .

Площадь всей пластины равна:

Для определения координат центра массы заданной пластины применяем выражения (21). Подставим значения всех известных величин в данном уравнении, получим

Согласно полученных значений координат центра массы пластины укажем точку С на рисунке. Как видно, центр массы (геометрическая точка) пластины находится за ее пределами.

Способ дополнения . Этот способ есть частичным случаем способа разделения. Он может применяться к телам, которые имеют вырезы (пустоты). Причем, без вырезанной части, положение центра массы тела известно. Рассмотрим например применение такого метода.

Пример 2. Определить положение центра массы веса круглой пластины радиусом R, в которой есть вырез радиусом r (рис.10). Расстояние .

Решение : Как видим, из рис.10 центр массы пластины лежит на оси симметрии пластины, то есть на прямой , поскольку эта прямая есть осью симметрии. Таким образом, для определения положения центра массы этой пластины необходимо определить только одну координату , поскольку вторая координата будет расположена на оси симметрии и уравновешивает нулевые. Покажем оси координат , . Примем, что пластина складывается из двух тел – из полного круга (как будто без выреза) и тела, которое как будто выполнено с вырезом. В принятой системе координат координаты для указанных тел будут равны: .Площади тел равны: ; . Общая площадь всего тела будет равна разнице между площадями первого и второго тела, а именно

3 Приложения двойных интегралов

3.1 Теоретическое введение

Рассмотрим приложения двойного интеграла к решению ряда геометрических задач и задач механики.

3.1.1 Вычисление площади и массы плоской пластины

Рассмотрим тонкую материальную пластину D , расположенную в плоскости Оху . Площадь S этой пластины может быть найдена с помощью двойного интеграла по формуле:

3.1.2 Статические моменты. Центр масс плоской пластины

Статическим моментом M x относительно оси Ox материальной точки P (x ;y ), лежащей в плоскости Oxy и имеющей массу m , называется произведение массы точки на ее ординату, т.е. M x = my . Аналогично определяется статический момент M y относительно оси Oy : ­ ­ ­ M y = mx . Статические моменты плоской пластины с поверхностной плотностью γ = γ (x, y ) вычисляются по формулам:

Как известно из механики, координаты x c , y c центра масс плоской материальной системы определяются равенствами:

где m – масса системы, а M x и M y – статические моменты системы. Масса плоской пластины m определяется формулой (1), статические моменты плоской пластины можно вычислить по формулам (3) и (4). Тогда, согласно формулам (5), получаем выражение для координат центра масс плоской пластины:

Типовой расчет содержит две задачи. В каждой задаче задана плоская пластина D , ограниченная линиями, указанными в условии задачи. Г (x,y ) – поверхностная плотность пластины D . Для этой пластины найти: 1. S – площадь; 2. m – массу; 3. M y , M x – статические моменты относительно осей Оy и Ох соответственно; 4. , – координаты центра масс.

3.3 Порядок выполнения типового расчета

При решении каждой задачи необходимо: 1. Выполнить чертеж заданной области. Выбрать систему координат, в которой будут вычисляться двойные интегралы. 2. Записать область в виде системы неравенств в выбранной системе координат. 3. Вычислить площадь S и массу m пластины по формулам (1) и (2). 4. Вычислить статические моменты M y , M x по формулам (3) и (4). 5. Вычислить координаты центра масс , по формулам (6). Нанести центр масс на чертеж. При этом возникает визуальный (качественный) контроль полученных результатов. Численные ответы должны быть получены с тремя значащими цифрами.

3.4 Примеры выполнения типового расчета

Задача 1. Пластина D ограничена линиями: y = 4 – x 2 ; х = 0; y = 0 (x ≥ 0; y ≥ 0) Поверхностная плотность γ 0 = 3. Решение. Область, заданная в задаче, ограничена параболой y = 4 – x 2 , осями координат и лежит в первой четверти (рис. 1). Задачу будем решать в декартовой системе координат. Эта область может быть описана системой неравенств:

Рис. 1

Площадь S пластины равна (1): Так как пластина однородная, ее масса m = γ 0 S = 3· = 16. По формулам (3), (4) найдем статические моменты пластины: Координаты центра масс находятся по формуле (6): Ответ: S ≈ 5,33; m = 16; M x = 25,6; M y = 12; = 0,75; = 1,6.

Задача 2. Пластина D ограничена линиями: х 2 + у 2 = 4; х = 0, у = х (х ≥ 0, у ≥ 0). Поверхностная плотность γ (x,y ) = у . Решение. Пластина ограничена окружностью и прямыми, проходящими через начало координат (рис. 2). Поэтому для решения задачи удобно использовать полярную систему координат. Полярный угол φ меняется от π/4 до π/2. Луч, проведенный из полюса через пластину, «входит» в неё при ρ = 0 и «выходит» на окружность, уравнение которой: х 2 + у 2 = 4 <=> ρ = 2.

Рис. 2

Следовательно, заданную область можно записать системой неравенств: Площадь пластины найдем по формуле (1): Массу пластины найдем по формуле (2), подставив γ (x,y ) = у = ρ sinφ :
Для вычисления статических моментов пластины используем формулы (3) и (4):
Координаты центра масс получим по формулам (6): Ответ: S ≈ 1,57; m ≈ 1,886; M x = 2,57; M y = 1; = 0,53; = 1,36.

3.5 Оформление отчета

В отчете должны быть представлены все выполненные расчеты, аккуратно выполненные чертежи. Численные ответы должны быть получены с тремя значащими цифрами.